Les lois de Zipf et de Mandelbrot |
 |
Les lois de Zipf et de Mandelbrot : origine et définition
Dans les années 1930, c’est-à-dire bien avant l’apparition des ordinateurs sous leur forme actuelle, Zipf a observé que la fréquence d’utilisation d’un mot dans un texte volumineux était inversement proportionnelle à son rang. Ainsi, si le mot le plus fréquent apparaît 150 fois dans un texte, les mots se classant aux deuxième et troisième rangs en ce qui concerne leur fréquence apparaîtront respectivement 75 fois et 50 fois. (Voir l’article correspondant dans Wikipédia.)
Selon la loi de Zipf, si 
est le 
mot le plus fréquent dans un texte, il doit alors avoir la fréquence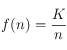 
où 
est une constante (indépendante de ).
Le graphique suivant représente la courbe 
.
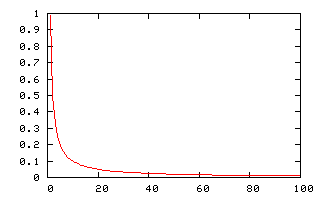
Il existe une généralisation de la loi de Zipf, appelée loi de Mandelbrot, selon laquelle la fréquence du mot ayant le rang est 
où 
sont des constantes. Un ensemble de documents peut obéir à une loi comme celle-ci : 
qui représente la fréquence du mot ayant le rang dans l’ensemble des documents [1].
Étant donné la distribution des fréquences, il est parfois difficile de dire s’il s’agit bel et bien d’une distribution de Zipf car d’autres distributions y ressemblent beaucoup, comme la distribution log-normale.
est grand, on peut alors
utiliser la formule 
(
est la constante d’Euler-Mascheroni, 0,5772156649).
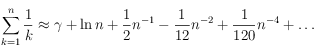Dans tous les cas, la somme des probabilités doit être 1. On peut donc, de cette manière, contraindre la valeur des constantes.
La « Long Tail »
Un nombre étonnant de distributions prennent la forme d’une distribution de Zipf (aussi appelée power law). Il semble que, souvent, quand on demande à des personnes de choisir parmi un grand ensemble d’articles, on obtient une distribution de Zipf. Au premier abord, on pourrait conclure que cela signifie que les personnes tendent toutes à choisir les mêmes 2 ou 3 articles, mais en y regardant de plus près, on constate que les choix minoritaires, quand on les regroupe, forment une masse imposante.
Prenons un cas un peu artificiel... supposons qu’on ait le choix entre 2000 produits. Supposons également qu’on constate qu’un client va acheter avec une probabilité 
le e produit le plus populaire. Quelle est la probabilité qu’il achète un produit qui ne fasse pas partie des dix plus populaires ?
Quelle est la probabilité que le produit acheté ne soit pas dans les 20 plus populaires ?
Nous constatons qu’en vertu de la loi de Zipf, s’il y a une grande variété de choix, ceux qui sont les moins populaires forment ensemble le groupe le plus populaire (64 ou 56 % dans le cas de notre exemple) !
Le contraire de cette assertion donne un résultat d’ailleurs assez surprenant : cela reviendrait à affirmer que pour remporter du succès, un libraire n’a qu’à proposer les 20 titres les plus populaires dans son établissement...
Nous verrons plus loin dans le cadre du cours qu’il faut établir un lien entre la loi de Zipf et les mesures de qualité des systèmes de recherche d’informations. En effet, nous pourrions croire, à tort, que la population ne veut que 2 ou 3 sources d’informations très fiables (et donc, une très grande précision de recherche) mais, dans les faits, suffisamment de personnes veulent d’autres sources d’informations pour que ce besoin soit pris en compte.
Plus la société est informatisée, plus l’accès aux informations est facilité, plus les choix moins populaires deviennent accessibles et donc importants. Pour les fournisseurs de services, il est important d’assurer une bonne couverture des sources d’informations et des produits.
Références :
– Chris Anderson, The Long Tail : Why the Future of Business Is Selling Less of More, New York, Hyperion, juillet 2006, 256 p.
– Chris Anderson, The Long Tail, Wired Magazine, vol. 12, no 10, 2004.
L’urne de Polya
On fait généralement un lien entre le comportement des consommateurs et le problème de l’urne de Polya. Le problème de l’urne est posé ainsi. Au départ, on a une urne contenant une boule de chaque couleur. On pige une boule au hasard. On duplique la boule ainsi tirée en faisant une copie, et on remet les deux copies dans l’urne. Au bout de plusieurs répétitions de ce processus, on trouvera dans l’urne, une certaine fraction de boules de chaque couleur et cette fraction sera stable au fil du temps. Ces fractions ne sont pas uniformes : certaines couleurs seront plus populaires.
Par exemple, imaginons qu’une communauté compte dans ses rangs trois chanteurs rock d’égal talent. Chaque chanteur est représenté par une boule d’une couleur distincte dans l’urne, les boules étant des fans. Si au départ on commence avec un fan pour chaque chanteur, on peut alors penser que l’action de choisir une boule au hasard correspond à ce qui se passe quand on cherche de la bonne musique : on consulte ses voisins et on choisit, aléatoirement, une des recommandations. Avec ce modèle, on obtiendra comme résultat que la popularité des trois chanteurs ne sera pas nécessairement égale au bout d’un moment. Un des chanteurs, parce qu’il a acquis plus rapidement des fans au début, deviendra beaucoup plus populaire que les autres.
Il est donc possible de penser que des produits qui ne sont pas très populaires sont simplement victimes de l’effet de l’urne de Polya.
Comment savoir si on a une distribution de Mandelbrot ? (matériel optionnel)
Déterminer à l’œil nu si on a une distribution de Mandelbrot peut être
difficile en pratique. Heureusement, il existe des techniques statistiques rigoureuses pour faire ce type de vérification [2].
Ce qu’il faut absolument retenir
Dans le contexte de ce cours, il est rare que tous les événements soient équiprobables. Le plus souvent, en recherche d’informations, on trouve des distributions qui ressemblent à la distribution de Zipf.
[1] La différence entre $f(n)= K/n^0,99$ et $f(n)= K/n^1,0$ est petite, mais ce n’est qu’un exemple.
[2] Aaron Clauset, Cosma Rohilla Shalizi, M. E. J. Newman, Power-law distributions in empirical data, arXiv:0706.1062v1.
