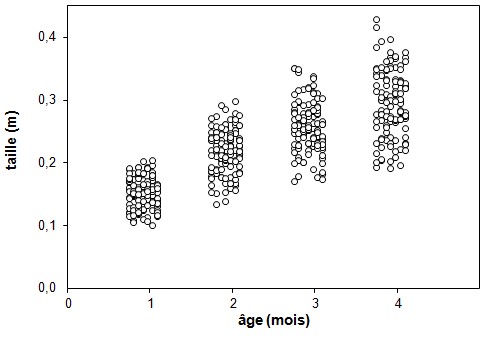
On l'a dit, contrairement aux autres dispositifs, un graphique permet d'afficher un très grand nombre de valeurs sans qu'il soit nécessaire d'accroître sa taille. Ainsi, le graphique de la figure 4 contient des centaines de points sans que cela nuise à son efficacité; en fait, seul un graphique permet de représenter de manière appropriée ce type de données.
Cependant, il peut arriver que les points soient si nombreux, du moins dans certaines régions du graphique, qu'ils se superposent en bonne partie. Cela se produit lorsque les quantités mesurées sont très variables ou mal définies, ce qui correspond à une incertitude de type B importante.
Ainsi, les valeurs de la taille des plantes qui figuraient dans les exemples de dispositifs proposés dans ces textes étaient en fait la moyenne des mesures effectuées à chaque mois sur un grand nombre de plants dont les tailles pouvaient être très différentes les unes des autres.
L'incertitude (égale dans ce cas à deux fois l'écart-type de la distribution des mesures) donnait d'ailleurs une idée de l'éventail des valeurs mesurées. Mais cela demeure une représentation simplifiée des mesures. En principe, un graphique permettrait de toutes les représenter, ce qui fournirait un portrait complet de l'expérimentation. La figure 12 représente cette situation, avec une douzaine de mesures à chaque mois, ce qui pourrait correspondre à une pré-expérimentation. Notez que les points ont été légèrement dispersés horizontalement de part et d'autre de leur vraie position afin de mieux les distinguer.
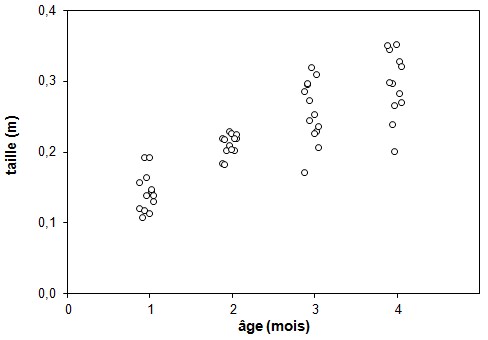
Figure 12. Taille des plants (N = 12) à chacun des quatre mois de la pré-expérimentation. Les points ont été légèrement déplacés horizontalement pour limiter les recouvrements.
Mais dès que le nombre de valeurs devient important, un tel graphique risque d'être plutôt inutile, même si on disperse les points horizontalement, comme le montre la figure 13, où l'on compte plus d'une centaine de mesures à chaque mois.
Figure 13. Taille des plants (N = 100) à chacun des quatre mois de l'expérimentation. Les points ont été légèrement déplacés horizontalement pour limiter les recouvrements.
Cependant, il existe un compromis entre afficher tous les points et afficher uniquement la moyenne et l'incertitude : le graphique à boîtes et moustaches, souvent appelé « graphique à boîtes » tout court (box and whisker plot et box plot en anglais, respectivement).
L'idée est de remplacer un ensemble des points par une figure (la « boîte » et ses « moustaches ») appelée diagramme de Tukey, du nom de son inventeur. Celle-ci, à la manière d'un histogramme (voir texte C6, section 4), fournit des informations plus détaillées sur la distribution des mesures que la simple combinaison moyenne-incertitude.
Différentes versions du graphique à boîtes ont été proposées : avec ou sans moustaches, avec divers critères pour établir la longueur de celles-ci; avec affichage ou non des points individuels très éloignés de la moyenne (associés aux valeurs dites aberrantes).
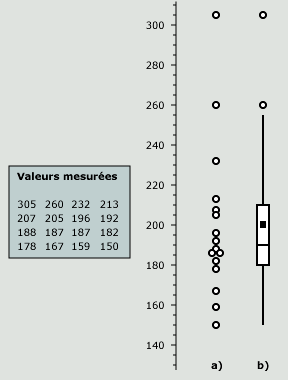
La figure 14b illustre celle qui a été retenue pour ce cours. En cliquant dans la figure, une version interactive de celle-ci s'ouvrira dans une nouvelle fenêtre et vous permettra d'obtenir des explications sur les diverses caractéristiques de ce diagramme, fondées sur les notions de médiane (la valeur qui sépare une distribution en deux groupes égaux) et de quartiles (les trois valeurs qui la séparent en quatre groupes égaux). Les fonctions calculant ces valeurs sont disponibles dans Excel, soit MEDIANE(XX:YY) et QUARTILE(XX:YY;n), où XX:YY désigne la série de valeurs et n = 1, 2 ou 3 pour les limites de quartiles nommés Q1, Q2 (identique à la médiane) et Q3.
La boîte proprement dite est associée aux valeurs comprises dans les deux quartiles centraux, soit entre Q1 et Q3; elle comprend donc la moitié des points. Sa hauteur est égale à l'interquartile Q, qui vaut Q3 - Q1.
La ligne à l'intérieur de la boîte indique la médiane (ou Q2) et le carré, la moyenne.
Les lignes verticales partant des deux extrémités de la boîte, appelées moustaches (whiskers en anglais), indiquent les zones où se trouvent les valeurs non aberrantes du premier ou du dernier quartile, c'est-à-dire situées à moins de 1,5 Q de la boîte. Dans la version retenue pour ce cours, elles s'arrêtent au dernier point quand celui-ci se trouve en deçà de 1,5 Q (c'est le cas de la moustache du bas dans la figure 14). Dans le fichier Excel de gabarits, une option vous permet toutefois de choisir entre cette option et celle d'une longueur fixe de 1,5 Q.
La valeur de 1,5 Q a été fixée de manière arbitraire. Quand la distribution des valeurs est normale, au sens statistique du terme (courbe en forme de cloche), cela signifie que les valeurs aberrantes compteront en moyenne pour un peu moins de 1 % du total des valeurs.
Figure 14. Boîte (ou digramme
de Tukey) représentant
les valeurs mesurées affichées dans
l'encadré, à gauche de l'axe.
Cliquez dans la figure ou sur le lien
suivant pour ouvrir dans une nouvelle fenêtre une
version interactive de la figure décrivant les
caractéristiques de la boîte.
Avec cet outil, nous pouvons refaire le graphique de la figure 13, qui devient alors beaucoup moins encombré. Il permet de conclure, par exemple, que certains plants d'un mois sont plus grands que d'autres de 4 mois, ou que la taille moyenne aux mois 2 à 4 est toujours supérieure à celle de 75 % des plants (Q3, le sommet de la boîte) un mois plus tôt.

Figure 15. Distribution de la taille des plants (N = 100) à chaque mois.
[Exemple de graphique à boîtes représentant un grand nombre de mesures pour chaque valeur d'une VI discrète]
Dans les cas où la VI est continue, ou qu'elle prend un grand nombre de valeurs, on peut avoir recours au même procédé : il suffit de regrouper les valeurs en un nombre restreint de séries couvrant chacune un intervalle de valeurs de la VI.
Par exemple, pour une série de mesures du taux d'activité durant une journée d'individus d'une colonie d'insectes (des fourmis, par exemple) et de la température moyenne au cours de la journée, qui donnerait un graphique comme celui de la figure 16, on peut regrouper les mesures en séries correspondant à des intervalles de température de 1 °C centrés à chaque valeur entière, pour obtenir le graphique à boîtes correspondant (figure 17).

Figure 16. Taux d'activité quotidien en fonction de la température moyenne.
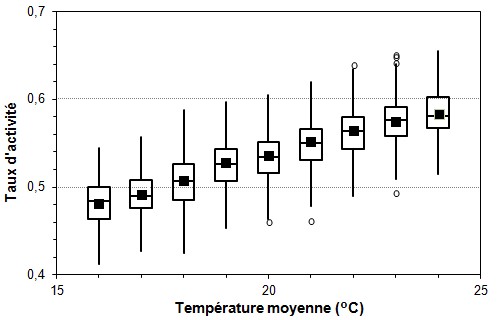
Figure 17. Distribution du taux d'activité quotidien en fonction de la température moyenne (valeurs regroupées en intervalles de 1 °C).
[Exemple de graphique à boîtes avec regroupement des valeurs d'une VI continue]
Le regroupement est choisi de manière à ce que chaque groupe compte suffisamment de points pour que les quantités comme la médiane et les quartiles aient un sens, soit au moins une douzaine, mais idéalement beaucoup plus.
Soulignons qu'on peut également employer ce procédé avec une VI qualitative; on comptera alors une boîte pour chaque valeur de la VI, les boîtes étant également espacées horizontalement.
Pour terminer, précisons que tous les graphiques de ce texte ont été effectués à l'aide d'Excel (ce sont des copies d'écran), y compris les graphiques à boîtes, qui ne sont pas inclus dans les options offertes par ce logiciel. Je rends disponible, aux fins des activités et travaux notés, un fichier Excel qui comprend des gabarits pour tous ces types de graphiques avec des consignes pour leur utilisation.