|
|
|
|
|
1.
|
Introduction
|
|
Les diagrammes servent
à présenter des
données ou des résultats
quand toutes les variables
indépendantes sont qualitatives.
Ils peuvent aussi être
employés s'il y a une ou des VI
quantitatives discrètes
possédant un nombre limité
de valeurs.
Il existe plusieurs types
de diagrammes. Le principal est le
diagramme à barres. D'autres
types sont soit peu recommandables, car
plus difficiles à lire avec
précision (par exemple les
diagrammes en « pointes de
tarte »), soit peu
utilisés (par exemple, les
diagrammes à points, qui sont
pourtant un compromis intéressant
entre les diagrammes et les
graphiques).
Comme leur nom l'indique,
les diagrammes à barres sont
formés... de barres, verticales
(figure 1)
ou horizontales (figure 2).
Chaque barre est associée à
une valeur de la variable
indépendante (qualitative ou
quantitative discrète); la longueur
de la barre représente la valeur de
la variable dépendante
(quantitative et, en
général, continue).
Aucune des deux versions
n'est vraiment préférable du
point de vue de la facilité de
lecture, mais les diagrammes à
barres horizontales présentent
l'avantage de fournir plus d'espace pour
afficher les valeurs des variables
qualitatives. Cela permet d'inscrire des
mots plus longs, donc plus signifiants,
qui facilitent grandement la lecture.
Ainsi, dans la figure 1,
le lecteur doit consulter le texte pour
savoir ce que signifient les lettres
représentant les diverses
méthodes, dont les noms sont
beaucoup trop long pour être
affiché sous l'axe.
La présence des
lignes de fond (quadrillage) est
très importante pour éviter
les effets d'illusion d'optique dus
à la juxtaposition de barres de
longueurs différentes. Notons
également que les barres ont
été ordonnées selon
leur longueur, plutôt que
d'après l'ordre alphabétique
des lettres des méthodes, et que
les deux barres vers lesquelles on
désire attirer l'attention ont
été colorées
différemment.
Soulignons finalement que
l'utilisation de diagrammes en perspective
est à déconseiller.
|
|
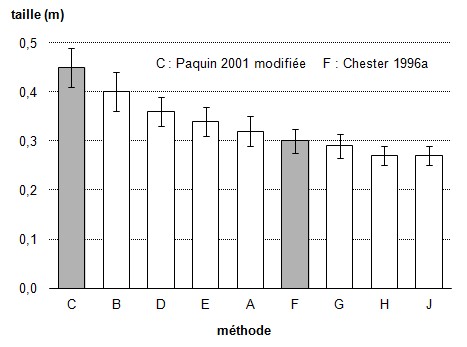
Figure 1.
Taille des plants de quatre mois pour
diverses méthodes de fertilisation.
[Exemple de diagramme à barres
verticales à 1 VI et
1 VD]
|
|
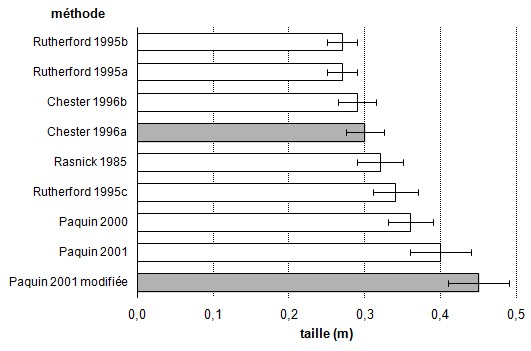
Figure 2.
Taille des plants de quatre mois pour
diverses méthodes de fertilisation;
mêmes données qu'à la
figure 1.
[Exemple de diagramme à barres
horizontales]
|
|
2.
|
Les diagrammes à
trois variables
|
|
On traite
différemment les diagrammes
à une et à deux variables
dépendantes (donc, avec
respectivement deux et une seule variable
indépendante).
Avec deux variables
dépendantes, on place simplement
côte-à-côte deux
diagrammes, un pour chaque VD. Ainsi, la
figure 3 montre un diagramme à
barres à 1 VI et 2 VD qui
présente, pour cinq
variétés de plants (la VI),
les différences de croissance selon
deux mesures (les VD) : la taille des
plants et la masse des feuilles. Remarquez
qu'on a employé une teinte
différente pour la moyenne, pour
bien la distinguer des valeurs
individuelles.
|
|
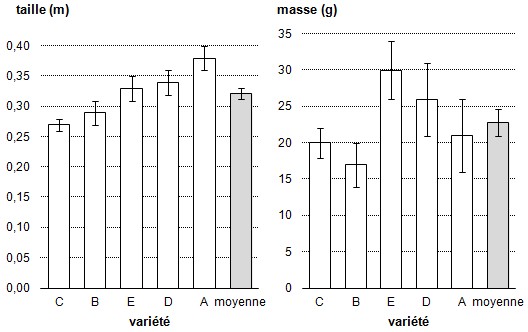
Figure 3.
Taille et masse des feuilles de 5
variétés de plants de quatre
mois. [Exemple de diagramme à
barres à 1 VI et
2 VD]
Avec une seule VD, mais deux VI, on
emploiera un diagramme avec des
séries (une pour chaque valeur de
la VI pour laquelle la comparaison est la
plus significative) de couleurs
différentes ou, pour l'impression
en noir et blanc, des tons de gris. La
figure 4 présente un diagramme
à barres à 2 VI et
1 VD, la VD la taille des plants et
les VI la variété et la
méthode de fertilisation (la
comparaison la plus significative,
identifiée par un renvoi
bibliographique).
|
|
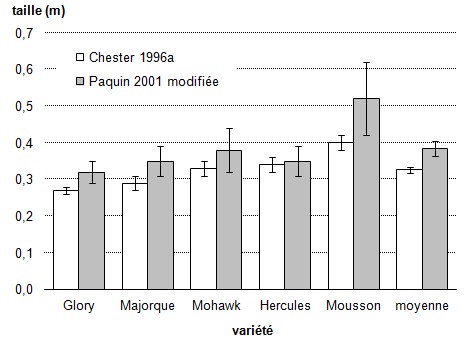
Figure 4.
Taille de 5 variétés de
plants de 4 mois pour les méthodes
de fertilisation décrites dans
Chester (1996a) et Paquin (2001), avec
modifications. [Exemple de diagramme
à barres à 2 VI et
1 VD, avec 2 tons de gris]
|
|
Dans ce diagramme, la comparaison se fait
le plus facilement entre les
résultats des deux méthodes
pour une même variété.
Si l'on désire plutôt
favoriser la comparaison entre les
variétés pour une même
méthode, on regroupera autrement
les variables; la teinte sera alors
associée à la valeur de
l'autre VI (la variété).
La figure 5
montre les mêmes données
qu'à la figure 4,
mais disposées de manière
à favoriser la comparaison entre
les variétés.
Il faut souligner ici que,
selon la qualité de l'imprimante ou
du photocopieur, il peut être
difficile de distinguer plus de 3 ou 4
tons de gris. On peut aussi employer des
trames (voir cette
version de la figure 5);
soulignons cependant que cette option a
disparu dans la version 2007 d'Excel, pour
réapparaître dans la
suivante.
En général,
des diagrammes comprenant plus de 3 ou 4
valeurs de VI associées à
des teintes, comme celui de la figure 5,
devraient être
réservés à une
présentation ou une diffusion en
couleurs; il vaut mieux alors employer des
couleurs au lieu des tons de gris, comme
dans cette version
en couleurs de la figure 5.
|
|
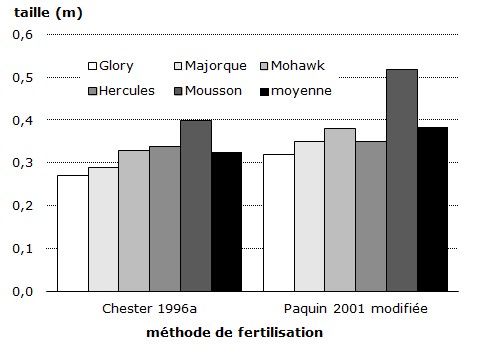
Figure 5.
Taille de 5 variétés de
plants de 4 mois pour deux méthodes
de fertilisation (même
données qu'à la figure 4,
sans l'incertitude). [Exemple de
diagramme à barres à
2 VI et 1 VD, avec 6 tons de
gris]
|
|
Cependant, même si on peut, du moins
selon mon expérience, distinguer
assez facilement jusqu'à une
dizaine de couleurs, quand elles sont
judicieusement choisies, et que les trames
passent mieux le test de l'impression ou
de la photocopie que les tons de gris, les
diagrammes deviennent difficiles à
lire dès que le nombre de barres
contiguës dépasse quatre ou
cinq.
Faites vous-même
l'exercice, en comparant la figure
ci-dessus et la version où les
séries sont regroupées
autrement de manière à
limiter le nombre de tons de gris
(figure
4, dans une nouvelle fenêtre),
en vous demandant laquelle est la plus
facile à interpréter, ou
encore laquelle des deux permet de mieux
démontrer que la méthode
Paquin 2001 modifiée est
supérieure à la
méthode Chester 1996a.
|
|
3.
|
Les diagrammes à
trois variables indépendantes
(VI)
|
|
Pour représenter
trois variables indépendants, on
juxtapose verticalement des diagrammes
à barres horizontales à deux
VI, comportant des échelles
identiques. Ainsi, pour représenter
des séries de mesures comme celles
de la figure 5, mais
répétées à
chaque année, on placera l'un
au-dessus de l'autre des diagrammes
associés à chaque
année (figure 6).
On constate facilement
qu'avec l'augmentation du nombre de
séries, la présentation
graphique des données perd un peu
de son intérêt. Dans ce cas,
on pourrait penser qu'il serait amplement
suffisant de fournir le diagramme de la
moyenne des trois années
d'expérimentation.
|
|
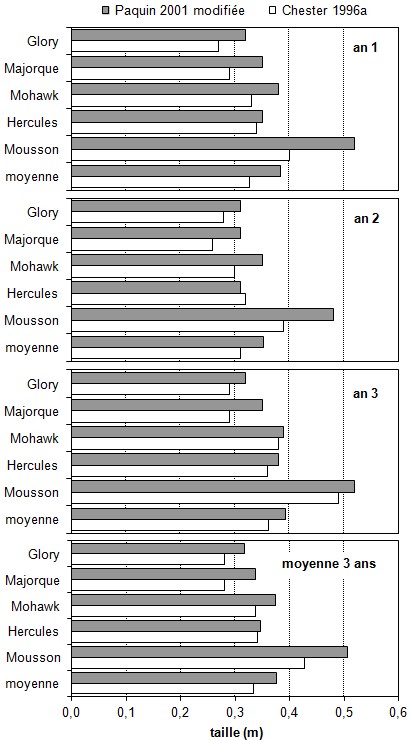
Figure 6.
Taille de 5 variétés de
plants de quatre mois pour 2
méthodes de fertilisation et 3
années d'expérimentation.
[Exemple de diagramme à barres
à 3 VI et 1 VD,
réparti dans quatre
fenêtres]
|
|
Finalement, une remarque
sur le fait que contrairement à une
pratique très répandue,
aucun des digrammes
présentés ici n'affiche les
valeurs numériques au bout des
barres. De l'avis des auteurs qui ont
étudié l'efficacité
des dispositifs de présentation,
avis que je partage, ces informations sont
très peu utiles, car le but d'un
diagramme est de fournir visuellement une
idée d'ensemble des valeurs et de
permettre des comparaisons entre certaines
d'entre elles. L'ajout des valeurs vient
brouiller le portrait, en obligeant le
lecteur à se demander s'il porte
son attention sur les longueurs des barres
ou sur les valeurs, ou les deux.
À mon avis, les
seules situations où cela pourrait
être indiqué
seraient :
|
|
-
|
quand les valeurs obtenues
sont très précises et que
l'atteinte de cette précision est
un des points forts de la recherche;
|
|
-
|
quand une des valeurs (par
exemple la plus grande) doit être
comparée à une valeur
standard ou limite, dont elle peut devenir
très proche; on pourrait dans ce
cas afficher seulement ces deux valeurs
numériques, tout en laissant les
autres barres sans valeurs.
|
|
La figure 7 illustre
une telle situation, au moyen du
même diagramme qu'à la
figure 2,
en supposant cette fois que l'incertitude
est très faible; en effet, selon ce
qu'on peut déduire du nombre de
chiffres significatifs affichés,
les rectangles d'incertitude seraient trop
petits (de l'ordre de 0,001 m) pour
être visibles.
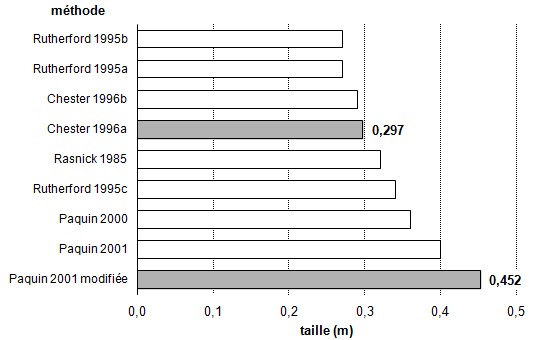
Figure 7.
Taille des plants de quatre mois pour
diverses méthodes de fertilisation;
mêmes données qu'à la
figure 1.
|
|
4.
|
Les histogrammes
|
|
Un histogramme est un type
particulier de diagramme à barres.
Il est utilisé dans les cas
où l'on a mesuré ou
déterminé la valeur d'une
variable (VD ou VI) continue pour chaque
élément d'un groupe et que
l'on désire représenter la
distribution des valeurs de cette
variable, c'est-à-dire de quelle
façon se répartissent
l'ensemble des valeurs.
Pour ce faire, on divise
l'éventail des valeurs de la
variable en un petit nombre
(généralement
inférieur à 10)
d'intervalles contigus, placés sur
un axe horizontal. On transforme ainsi la
variable originale, continue, en une
variable discrète possédant
moins de dix valeurs, correspondant
à chaque intervalle. Cette variable
joue le rôle d'une VI aux fins du
diagramme.
À chacune de ces
valeurs, donc à chaque intervalle,
on associe une barre de largeur
égale à l'intervalle et dont
l'aire représente le nombre
d'objets pour lesquels la valeur
mesurée fait partie de l'intervalle
(figure 8). La plupart du temps, on
choisit des intervalles égaux; la
hauteur des rectangles est alors
proportionnelle au nombre d'objets
associés à chaque
intervalle. Le nombre d'objets joue alors
le rôle d'une VD. Le nombre total
d'objets est indiqué dans le
diagramme et (ou) dans la
légende.
Lorsque c'est possible, il
est préférable de choisir
une combinaison de valeur minimale de la
VD et d'intervalle qui place la moyenne
près du centre d'un des
intervalles; cela facilite
l'interprétation des
caractéristiques de la
distribution.

Figure 8.
Distribution de la taille de plants de
quatre mois de la variété A
(N = 250;
moyenne = 52,6 cm;
écart-type = 5,1 cm).
[Exemple d'histogramme]
Ce genre de diagramme
permet de visualiser rapidement certaines
caractéristiques de la distribution
que ne révèlent pas toujours
clairement la simple donnée de la
moyenne et de l'écart-type :
intervalle(s) de valeurs comprenant la
majorité des objets; manière
dont les valeurs se concentrent autour de
cet intervalle; symétrie de part et
d'autre de celui-ci.
L'histogramme de la
figure 8, qui compte 7 intervalles,
représente une distribution de la
taille des plants dont la moyenne est 52,6
cm et l'écart-type 5,1 cm. On
observe que les tailles des plants se
situent entre 35 et 70 cm, mais se
concentrent en majorité entre 50 et
55 cm, intervalle qui compte à
lui seul plus du tiers des valeurs. Les
autres valeurs sont distribuées de
part et d'autre de ce groupe central de
manière assez
symétrique.
La figure 9 présente
une seconde distribution, dont la moyenne
et l'écart-type sont les
mêmes qu'à la figure 8, mais
qui présente une allure assez
différente. Les tailles se situent
maintenant entre 28 et 84 cm, mais
sont beaucoup plus concentrées
autour de la moyenne, l'intervalle 52
à 60 cm comptant plus de
60 % des valeurs.
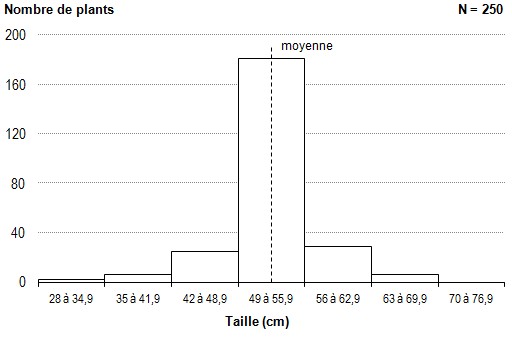
Figure 9.
Distribution de la taille de plants de
quatre mois de la variété B
(N = 250;
moyenne = 52,6 cm;
écart-type = 5,1 cm).
[Exemple d'histogramme illustrant une
distribution très concentrée
autour de la moyenne]
Finalement, l'histogramme
de la figure 10 présente une
troisième distribution, avec
toujours les mêmes moyenne et
écart-type. Les tailles, qui
varient entre 38 et 62 cm, se
répartissent plus largement autour
de la moyenne, et de manière
asymétrique, de sorte que
l'intervalle qui contient le plus de
valeurs (environ 29 % du total)
n'inclut pas la moyenne. Cette
distribution asymétrique se
caractérise par une queue à
gauche de la moyenne, qui étend
l'éventail des valeurs beaucoup
plus loin de celle-ci du côté
des petites valeurs.

Figure 10.
Distribution de la taille de plants de
quatre mois de la variété C
(N = 250;
moyenne = 52,6 cm;
écart-type = 5,1 cm).
[Exemple d'histogramme illustrant une
distribution asymétrique]
Pour terminer,
précisons que tous les diagrammes
de ce texte ont été
réalisés à l'aide
d'Excel (ce sont des copies
d'écran). Je rends disponible, aux
fins des activités et travaux
notés, un fichier
Excel qui comprend des gabarits pour
tous ces types de dispositifs graphiques,
avec des consignes pour leur utilisation.
On y retrouve entre autres un
système interactif de
génération d'histogramme. Il
est à noter que, dans Excel, on
désigne sous le nom d'histogramme
2D tout diagramme à barres
verticales.
|
|
5.
|
Les diagrammes à
boîte
|
|
Tout comme l'histogramme,
le diagramme à boîte
(appelé aussi diagramme à
boîte et moustaches, ou encore
diagramme de Tukey, du nom de son
inventeur) illustre la distribution des
valeurs d'une variable. Il fournit une
image moins détaillée que
l'histogramme, mais permet une meilleure
comparaison entre deux distributions (ou
plus).
Différentes versions
du diagramme à boîte ont
été proposées :
avec ou sans moustaches, avec divers
critères pour établir la
longueur de celles-ci; avec affichage ou
non des valeurs individuelles très
éloignées de la moyenne
(appelées valeurs
aberrantes).
La figure 11 illustre
celle qui a été retenue pour
ce cours. En cliquant dans la figure, une
version interactive de celle-ci s'ouvrira
dans une nouvelle fenêtre et vous
permettra d'obtenir des explications sur
les diverses caractéristiques de ce
diagramme, fondées sur les notions
de moyenne, de
médiane (soit le nombre,
noté Q2, tel que la moitié
des valeurs lui sont inférieures et
l'autre moitié, supérieures)
et de quartiles (les trois nombres,
notés Q1, Q2 et Q3, tels que le
quart, la moitié et les
trois-quarts lui sont inférieurs).
Les fonctions calculant ces nombres sont
disponibles dans Excel, soit
MEDIANE(XX:YY) et
QUARTILE(XX:YY;n), où XX:YY
désigne la série de valeurs
et n vaut 1, 2 ou 3 selon
qu'on désire obtenir Q1, Q2 ou Q3.
Les fonctions QUARTILE(XX:YY;2) et
MEDIANE(XX:YY) fournissent donc le
même résultat.
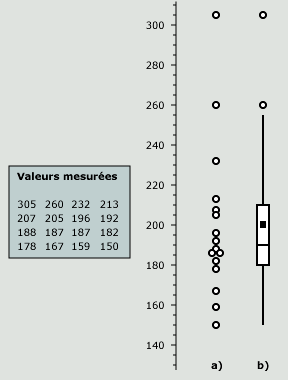
Figure 11. Points
individuels (a) et diagramme à
boîte (b) représentant les
valeurs mesurées, affichées
dans l'encadré à gauche de
l'axe. Cliquez dans la figure ou sur le
lien
suivant pour ouvrir dans une nouvelle
fenêtre une version interactive de
la figure décrivant les
caractéristiques du diagramme.
La boîte proprement
dite est associée aux valeurs
comprises dans les deux quartiles
centraux, soit entre Q1 et Q3; elle
comprend donc la moitié des points.
Sa hauteur est égale à
l'interquartile Q, qui vaut
Q3 - Q1.
La ligne à
l'intérieur de la boîte
indique la médiane (ou Q2) et le
carré, la moyenne.
Les lignes verticales
partant des deux extrémités
de la boîte, appelées
moustaches (whiskers en anglais),
indiquent les zones où se
retrouvent les valeurs non aberrantes du
premier ou du dernier quartile,
c'est-à-dire situées
à moins de 1,5 Q de la
boîte. Dans la version retenue pour
ce cours, elles s'arrêtent au
dernier point quand celui-ci se trouve
à moins de 1,5 Q de la
boîte; c'est le cas de la moustache
du bas dans la figure 11, qui est par
conséquent plus courte que celle du
haut. Dans le fichier Excel de gabarits,
une option vous permet de choisir entre
cette option et celle d'une longueur fixe
de 1,5 Q.
Cette valeur de 1,5 Q
a été fixée de
manière arbitraire. Quand la
distribution des valeurs est normale, au
sens statistique du terme (courbe en forme
de cloche), cela signifie que les valeurs
aberrantes compteront en moyenne pour un
peu moins de 1 % du total.
Avec cet outil, nous
pouvons comparer de manière plus
détaillée deux
résultats présentés
à la figure 4,
soit la taille des plants de
variété Mohawk selon deux
méthodes de fertilisation. Ainsi,
la figure 12, qui combine deux
diagrammes à boîte, permet de
conclure que si la méthode Paquin
2001 modifiée produit de meilleurs
résultats (ce que
révélait déjà
la figure 4), environ le quart des
plants traités avec cette
méthode (valeurs situées
sous la boîte) ne sont pas vraiment
plus grands. Un des plants traités
avec cette méthode est même
le plus petit de l'ensemble. On remarque
également que la méthode
Chester 1996a fournit une distribution
très
« pointue »,
c'est-à-dire concentrée
autour de la médiane (ou de la
moyenne), avec plusieurs valeurs
aberrantes, alors que l'autre
méthode produit une distribution
plus étendue.
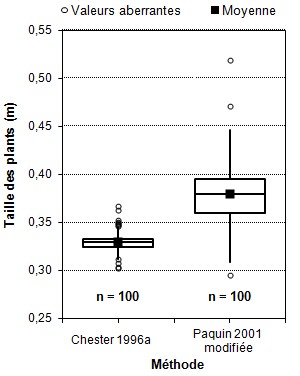
Figure 12. Taille
des plants pour deux méthodes de
fertilisation. [Exemple de dispositif
regroupant deux diagrammes à
boîte]
Note. Toutes les
figures de cette page sont des copies
d'écran de diagrammes
réalisés avec Excel, y
compris les diagrammes à
boîtes, qui ne sont pas inclus dans
les options offertes par ce logiciel. Je
rends disponible, aux fins des
activités et travaux notés,
un fichier
Excel qui comprend des gabarits pour
tous les types de dispositifs graphiques,
accompagnés de consignes
d'utilisation.
|
|
|
