|
|
|
|
|
1.
|
Introduction
|
|
Les graphiques sont employés quand au
moins une des VI est quantitative (continue ou
discrète) et, idéalement, qu'elle compte au
moins une dizaine de valeurs.
Ils conviennent
particulièrement :
|
|
-
|
pour illustrer une tendance,
c'est-à-dire de quelle façon la VD varie en
fonction de la VI, éventuellement pour chaque valeur
ou combinaison de valeurs de la ou des autres VI;
|
|
-
|
pour estimer l'adéquation d'un
modèle mathématique, théorique ou
empirique, décrivant la relation entre la VD et la ou
les VI; ce modèle étant
représenté par une ou des courbes sur le
graphique;
|
|
-
|
pour déterminer s'il y a une
corrélation entre deux variables, dont on ne sait pas
a priori si l'une est liée à l'autre, ou
l'influence.
|
|
Les graphiques sont aussi très utiles
pour mettre en évidence des anomalies, par exemple,
une valeur s'écartant de façon
exagérée de ce que suggère l'allure
générale des résultats ou le
modèle mathématique.
Dans un graphique, chaque couple de valeurs
de la variable indépendante (VI), ou d'une
combinaison de VI, et de la variable dépendante (VD)
est représenté par un point. Lorsque l'on
désire afficher les incertitudes sur la valeur des
variables, on les représente par des rectangles
d'incertitude, qui sont en fait des lignes dont les
longueurs indiquent les grandeurs de l'incertitude, selon
l'échelle de chaque axe (figure 1b). Dans les
cas particuliers (mais fréquents) où
l'incertitude sur une des variables est négligeable
ou trop faible pour être visible à
l'échelle du graphique, le rectangle se réduit
à une simple ligne verticale (figure 1a) ou
horizontale (figure 1c).
 Figure 1
Rectangles d'incertitude, avec incertitude : sur la VD seulement (a), sur les deux variables (b) et sur
la VI seulement (c). Figure 1
Rectangles d'incertitude, avec incertitude : sur la VD seulement (a), sur les deux variables (b) et sur
la VI seulement (c).
Les caractéristiques d'un graphique
dépendent du nombre et du type de variables qu'il
contient.
Passons donc en revue les principaux types de
graphiques. Veuillez noter que, les quantités
représentées sur les graphiques sont des
données simulées, sauf mention contraire (dans
ce cas, elles sont tirées de la thèse de
doctorat de l'auteur).
|
|
2.
|
Les graphiques à une variable
dépendante (VD)
|
|
Le graphique le plus simple (figure 2)
est celui qui ne comprend qu'une seule variable
dépendante (VD) et une seule variable
indépendante (VI). Ici, il y a en fait deux autres VI
(la variété et la dose), mais on ne cherche
pas à illustrer leur influence.
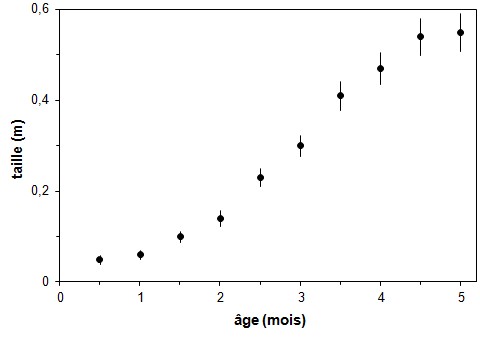
Figure 2. Taille des
plants de la variété Glory en fonction de
l'âge, dose optimale. [Exemple de graphique à
1 VI et 1 VD]
|
|
Le cadre dans lequel sont affichés les
points est appelé fenêtre des
données. Les côtés de celle-ci,
appelés axes, portent des divisions et
sous-divisions. Ces divisions, qui doivent être en
nombre restreint (normalement entre 3 et 6), affichent des
nombres (appelés étiquettes) couvrant
la gamme des valeurs des variables.
Par convention, la VI est portée sur
l'axe horizontal (ou abscisse) et la VD sur l'axe
vertical (ou ordonnée). Le nom et les
unités de chaque variable sont affichés au
centre de l'axe correspondant. Si l'on préfère
ne pas tourner le nom de la VD, on peut aussi afficher
celui-ci au-dessus du coin gauche de la fenêtre de
données, à l'horizontale.
Afin d'éviter que des points ne
risquent d'être masqués, les divisions et
sous-divisions sont placées à
l'extérieur de la fenêtre des données,
et les extrémités de celle-ci dépassent
les valeurs extrêmes des variables.
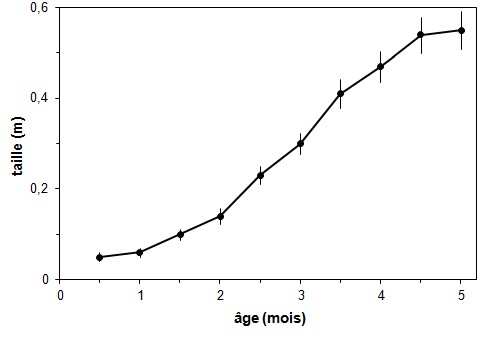
Pour mettre en évidence la progression
des valeurs, on peut relier les points successifs par des
segments de droite, comme dans la figure 3a, ou encore
tracer des courbes régulières, appelées
courbes de tendance, passant le plus possible au
voisinage des points (figure 3b).
|
|
a)
|
|
|
b)
|
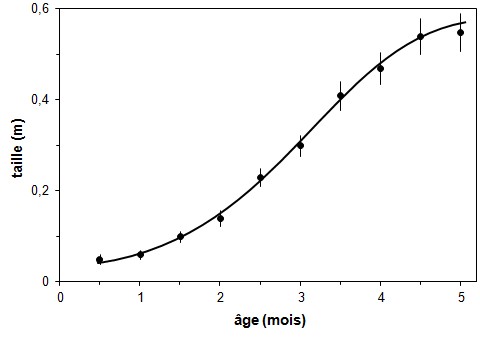
Figure 3.
Mêmes données qu'à la figure 2. [Exemples de graphiques à
1 VI et 1 VD avec points reliés (a) et
courbe de tendance (b)]
|
|
Ces segments et ces courbes ont pour but de faciliter la
perception des tendances; un trait plus épais que
celui du cadre et des divisions est normalement
employé.
Un graphique permet d'afficher sans
problème un très grand nombre de couples de
valeurs de variables, comme l'illustre la figure 4, qui
compte plus d'une centaine de points. La présence de
segments reliant les points est essentielle dans ce type de
graphique, soit lorsque les valeurs de la VD
présentent des fluctuations rapides mais que celles
de la VI sont régulièrement espacées
(quand la VI est le temps, on parle dans ce cas de
série chronologique).
On remarquera en outre le recours à
une échelle verticale logarithmique qui met en
évidence les fluctuations aux faibles
intensités, concentrées près du centre
et des bords du faisceau. Une échelle logarithmique
est employée quand la valeur maximale est telle que
les différences entre les plus petites valeurs que
l'on veut représenter deviennent peu perceptibles.
Elle est utile aussi lorsqu'on désire effectuer des
comparaisons en pourcentage, car des distances égales
le long de l'axe logarithmique correspondent à des
pourcentages égaux de variation.
Vous remarquerez que des droites
pointillées ont été tracées dans
la fenêtre des données. Elles indiquent des
valeurs de référence utiles à la
lecture du graphique. Ici, on a choisi la position
zéro et deux positions symétriques par rapport
à celle-ci, ce qui permet de visualiser plus
facilement l'asymétrie de la distribution.
|
|
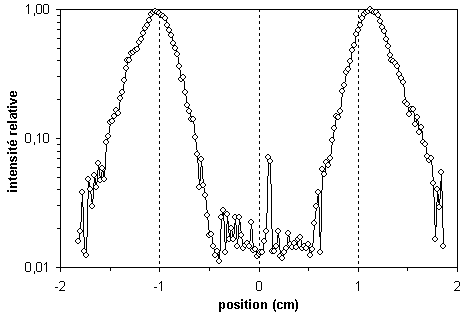
Figure 4 Intensité
d'un faisceau en fonction de la position horizontale
(données réelles). [Exemple de graphique de type
série chronologique avec points
reliés]
|
|
Lorsqu'une des valeurs dépasse très largement
les autres, ou encore que celles-ci se concentrent en deux
ou trois groupes distincts relativement
éloignés, il peut être utile
d'interrompre carrément un axe pour sauter à
une nouvelle valeur, avec ou sans changement
d'échelle. Cette procédure peut d'ailleurs
être employée à la place d'une
échelle logarithmique.
Une telle interruption doit être
fortement signalée. Une bonne façon de le
faire est de juxtaposer plusieurs fenêtres des
données nettement séparées. Ce
procédé est très utile pour mettre en
évidence certaines parties du graphique. Ainsi, pour
les mêmes données qu'à la figure 4,
un double changement d'échelle (vertical et
horizontal; voir figure 5) donne un meilleur
aperçu de la partie centrale du graphique, qui
apparaît dans sa propre fenêtre des
données. Remarquez qu'aucune échelle
logarithmique n'a été employée.
|
|
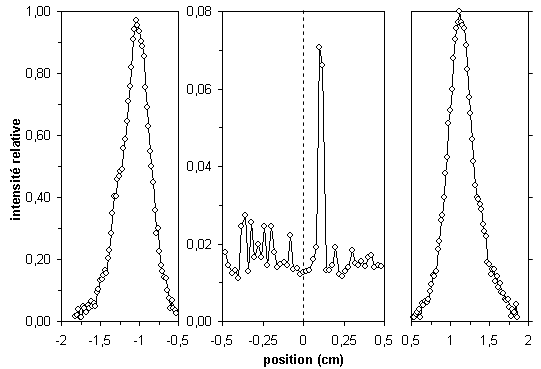
Figure 5 Mêmes
données qu'à la figure 4. [Exemple de graphique de type
série chronologique, avec fenêtre
scindée en trois, avec changement
d'échelle]
|
|
Les valeurs d'une seconde variable indépendante
(qualitative ou quantitative discrète) peuvent
être représentées sur le même type
de graphique (figure 6) par le recours à des
points de formes et de teintes différentes
associées aux valeurs de cette seconde VI.
|
|

Figure 6. Taille des
plants de la variété Glory en fonction de
l'âge,,
méthodes actuelle et optimale. [Exemple de graphique à
2 VI et 1 VD avec points reliés]
|
|
Dans ce type de graphique, les traits ou
courbes de tendance sont très utiles pour distinguer
les séries, surtout lorsque qu'elles ne sont pas bien
séparées, comme dans la figure 6. Il
convient alors d'utiliser pour chaque série de traits
et de points un style différent. Pour les graphiques
en couleurs, on choisira évidemment la même
couleur pour les points et les traits; pour les graphiques
destinés à l'impression ou la photocopie, il
est suggéré de ne pas employer de tons de
gris, mais de distinguer les points par leur forme, en
alternant pour chaque forme entre les variantes noire et
blanche, et les traits par le type de pointillé,
comme dans la figure 7.
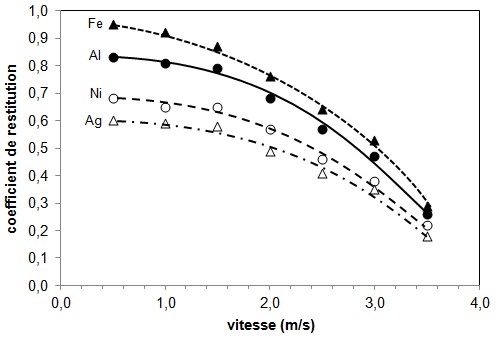
Figure 7. Coefficient de
restitution de sphères de divers matériaux en
fonction de la vitesse d'impact. [Exemple de graphique à
2 VI et 1 VD avec 4 séries et courbes de
tendance]
Au-delà de quatre ou cinq
séries, ou encore lorsque les séries
empiètent trop les unes sur les autres, il peut
être préférable de recourir à des
fenêtres des données juxtaposées
verticalement, contenant chacune une seule série et
comportant des axes horizontaux identiques.
|
|
3.
|
Les graphiques à deux variables
dépendantes (VD)
|
|
Lorsqu'il y a deux VD possédant des
gammes de valeurs, voire des unités
différentes, on peut associer chacun des deux axes
verticaux à l'une d'elles (figure 8), en
indiquant bien à quelle série de points
correspond chaque axe.
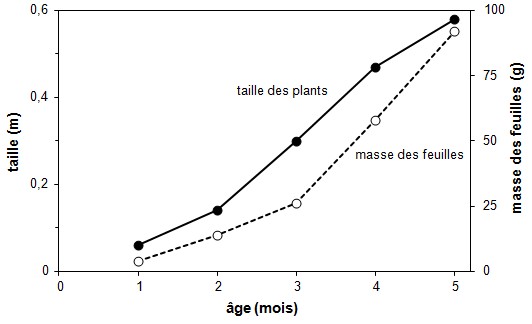
Figure 8. Taille et masse des
feuilles en fonction de l'âge des plants. [Exemple de graphique à 1 VI et
2 VD, avec double échelle]
|
|
Dans ce type de graphique, lorsqu'on désire comparer
l'importance des variations relatives (en pourcentage) des
deux VD, il est conseillé de faire partir les deux
axes de zéro, ou encore de choisir le même
rapport maximum-minimum pour les deux échelles. En
effet, comme le montre la figure 9, par le simple jeu
d'un changement du rapport maximum/minimum des
échelles, on peut donner l'impression que n'importe
quelle des deux VD varie beaucoup plus que l'autre en
fonction de la VI.
|
|
a)
|
|
|
b)
|

|
|
c)
|
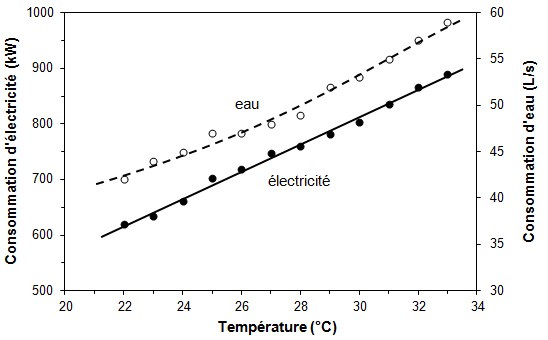
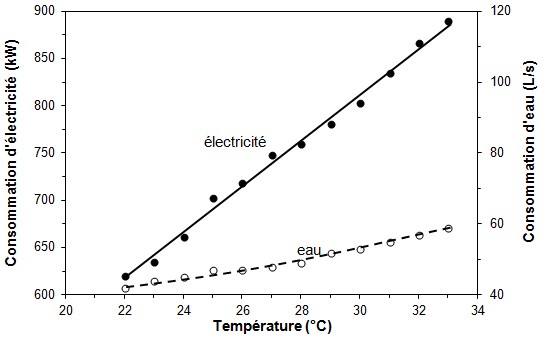
Figure 9. Taux de consommation
d'électricité et d'eau en fonction de la
température. [Trois versions d'un graphique
à 1 VI et 2 VD à double échelle.
Dans les deux premiers (a et b), le rapport maximum-minimum
des échelles diffère pour les deux axes
verticaux]
Ainsi, le premier graphique (figure 9a)
suggère que le taux de consommation moyenne
d'électricité augmente beaucoup plus que le
taux de consommation d'eau avec la température, alors
que le second (figure 9b), qui présente exactement
les mêmes données, suggère plutôt
l'inverse. Le troisième graphique (figure 9c), dont
le rapport maximum-minimum est le même (soit 2) pour les
deux axes verticaux, montre bien que les deux VD varient
sensiblement du même pourcentage en fonction de la VI
dans l'intervalle représenté.
|
|
4.
|
Courbes théoriques et valeurs
mesurées
|
|
Lorsqu'on associe un modèle
mathématique au phénomène
représenté par les données, les
courbes théoriques correspondantes sont
tracées sur le graphique (voir figure 10 et
fenêtre du haut du graphique de la figure 11),
de la même façon que les courbes de tendance.
Cependant, à la différence des courbes de
tendance, qui n'ont pour but que de guider l'œil en lui
fournissant un repère, les courbes théoriques
représentent les valeurs prédites ou fournies
par le modèle.
La nature du modèle et, si possible,
la valeur des paramètres qui lui permettent de bien
représenter le phénomène doivent
être mentionnées dans le texte, la
légende ou même à l'intérieur de
la fenêtre des données. Dans l'exemple de la
figure 10, le texte fournirait l'équation
où figure le paramètre a dont les
valeurs sont indiquées dans le graphique.
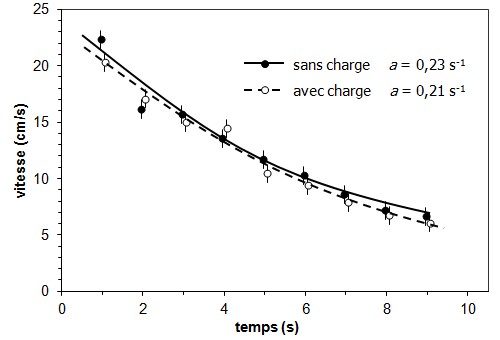
Figure 10. Vitesse d'un chariot
en fonction du temps, avec ou sans charge de 10 kg. [Exemple de graphique avec courbes
théoriques et affichage des paramètres du
modèle]
|
|
Si l'on veut mettre davantage en évidence
l'adéquation (ou la divergence) entre le
modèle et les points expérimentaux, on peut
juxtaposer au graphique présentant les valeurs
mesurées et la courbe théorique un
graphique des différences qui, comme son nom
l'indique, affiche la différence entre les valeurs
mesurées et celles que fournit le modèle. Ce
type de graphique sert à distinguer les écarts
aléatoires dus à l'incertitude sur les mesures
des écarts plus globaux qui traduisent la tendance
des valeurs mesurées, dans certaines régions
du graphique, à s'écarter du
modèle.
C'est ce qu'on a fait dans la figure 11,
où l'on a tracé dans le graphique des
différences une courbe de tendance qui permet de bien
distinguer les écarts globaux dans diverses parties
de la distribution et les variations aléatoires
(rapides) dues à l'incertitude sur les mesures, de
même que les régions où celle-ci semble
plus importante. Remarquez également que, comme dans
la figure 4 et la
figure 5 des droites
pointillées indiquent des valeurs de
référence (valeurs zéro et valeur
moyenne).
|
|
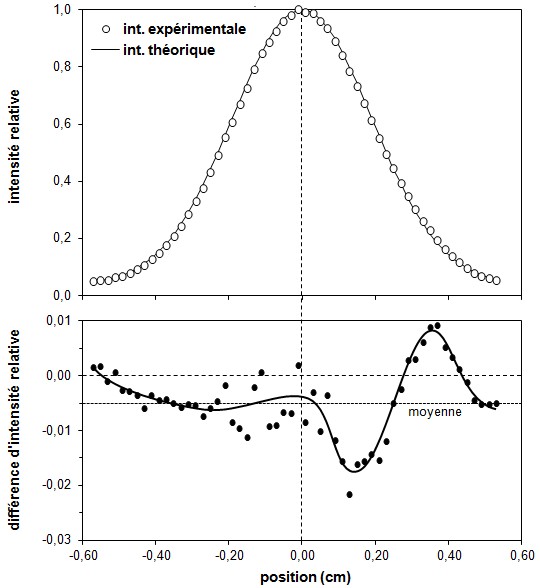
Figure 11. Haut :
intensité mesurée d'un faisceau en fonction de
la position horizontale (données réelles)
et courbe théorique correspondante (gaussienne avec
w = 0,38 cm).
Bas : différence entre intensité
mesurée et intensité théorique. [Exemple de comparaison
expérience-modèle à l'aide d'un
graphique des différences]
|
|
5.
|
Les graphiques de dispersion
|
|
Les graphiques de dispersion (appelés
aussi nuages de points, scatter plots en anglais)
sont des graphiques où, contrairement à tous
les graphiques illustrés plus haut :
|
|
-
|
les valeurs d'aucune des deux variables n'ont
été choisies ou fixées
(également espacées, par exemple) durant
l'expérimentation ou l'observation;
|
|
-
|
plusieurs valeurs d'une variable peuvent
être associées à une même valeur
de l'autre.
|
|
Il arrive même qu'il soit impossible de
déterminer quelle variable est la VI, ou même
si l'une dépend de l'autre. Les deux variables
peuvent en effet se révéler
complètement indépendantes, ou encore afficher
un lien (ou corrélation) dû simplement le fait
qu'elles dépendent toutes deux d'une troisième
variable, non considérée, qui est la
véritable VI.
La figure 12 illustre un grand nombre de
mesures (environ 400) du taux moyen d'activité de
fourmis et de la température moyenne au cours de la
journée, pour un grand nombre d'individus et de
jours. Bien que le taux d'activité varie
significativement pour une température donnée
(c'est ce qu'on entend par dispersion) on perçoit
bien une tendance régulière à
l'augmentation de l'activité en fonction de la
température, tendance soulignée par la droite
inclinée qui traverse le graphique
(générée, justement, par la fonction
« courbe de tendance » d'Excel). Dans ce
cas précis, les variables forment bien un couple
VI-VD, car il est très plausible de conclure que le
taux d'activité varie en fonction de la
température, l'inverse étant évidemment
impossible.
|
|
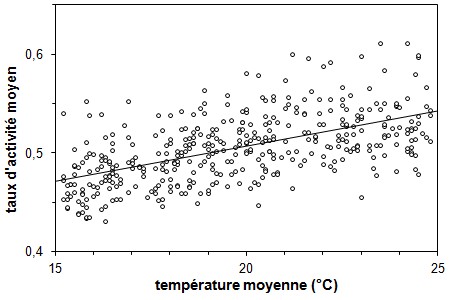
Figure 12. Taux d'activité
quotidien des fourmis en fonction de la température
moyenne. [Exemple de graphique de dispersion
à 1 VI et 1 VD]
Un tel graphique peut également
accommoder une seconde VI, discrète, si celle-ci ne
comporte que peu de valeurs. On emploie alors des types de
points différents (forme et teinte) pour distinguer
les valeurs de cette VI. La figure 13 illustre les
mêmes données que la précédente,
mais en indiquant de quelle colonie, parmi les quatre
étudiées, provenait chaque individu.
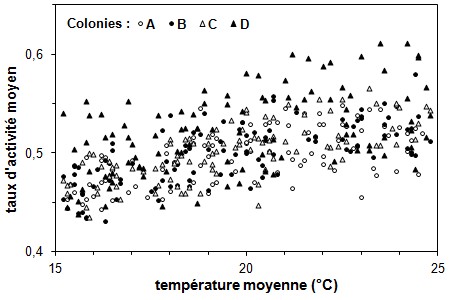
Figure 13. Taux d'activité
quotidien des fourmis en fonction de la température
moyenne, selon la colonie à laquelle elles
appartiennent. [Exemple de graphique de dispersion
à 2 VI et 1 VD]
On constate que les fourmis de la colonie D
se distinguent des autres : sur toute l'étendue
de la gamme de températures, les fourmis les plus
actives appartiennent à cette colonie.
Note. Toutes les figures de cette page
sont des copies d'écran de graphiques
réalisés avec Excel, en utilisant les gabarits fournis dans le cours.
|

|
|