C2 - La présentation des résultats numériques :
les grands principes

Les auteurs qui se sont intéressés à la présentation des résultats numériques ont proposé un certain nombre de principes devant présider à la conception des dispositifs - tableaux, diagrammes et graphiques - employés à cette fin.

Ces principes découlent de l'idée générale que ces dispositifs doivent servir à montrer les données et aider à les interpréter. Nous en retiendrons quatre.

Principe n° 1

Les éléments qui communiquent les données ou résultats, ou des informations sur ceux-ci, doivent être facilement perceptibles.
  

Trop de tableaux ou de graphiques n'atteignent pas leur but tout simplement parce qu'il est difficile de bien voir ce qu'ils contiennent. Cela est particulièrement fréquent lors des présentations orales avec projection sur écran; très souvent, une partie sinon l'ensemble des informations projetées sont tout simplement trop petites pour être correctement perçues depuis le fond de la salle.

On retrouve un phénomène semblable dans les graphiques ou diagrammes transformés en dessins bitmaps pour intégration à des documents numériques ou à des pages web; dans ce cas, c'est la limite de la résolution des écrans qui rend certaines informations difficiles à décoder, voire illisibles.

La figure 1 présente un graphique conçu pour être inclus dans un document imprimé, mais qui ne convient pas du tout à une présentation sur écran, et pas très bien à une page web (à moins d'offrir l'option d'une version agrandie). Et même si on offre un document en version PDF, qui permet de faire un zoom, il est préférable que le graphique soit bien lisible dans une page affichée à sa taille normale.

Figure 1. Exemple d'un graphique conçu pour un document imprimé mais peu approprié dans un autre contexte (projection sur écran, intégration dans une page web).

Pour obtenir un meilleur résultat quand on intègre un dispositif graphique dans un document imprimé (ou un document PDF), on créera dans le chiffrier (comme Excel) un dispositif beaucoup plus grand que la largeur permise d'après le format du document imprimé. La taille de l'image sera automatiquement réduite dans le traitement de texte après qu'on y ait collé la figure. Cela permet de bénéficier de la résolution de l'imprimante, très supérieure à celle de l'écran, et du zoom des lecteurs de PDF.

On portera cependant une attention particulière à la taille des inscriptions dans le graphique original afin d'éviter qu'elles ne deviennent illisibles après réduction, comme dans la figure 1. La règle générale est que la taille des caractères, un fois la figure réduite, ne devrait pas être inférieure à 8 points, ce qui signifie, par exemple, que des caractères d'au moins 16 points devront être employés dans un dispositif qui sera réduit de 50 % lors de la copie dans le traitement de texte. Pour les éléments graphiques tels les points, on pourra se fier en bonne partie à leur apparence à l'écran, dans le logiciel, si celui-ci possède une fonction de zoom qui permet de réduire la taille de l'affichage du même pourcentage.

Principe n° 2

Les aspects importants des résultats (en fait, ceux que l'on juge important de communiquer) doivent ressortir clairement, voire s'imposer d'emblée.

Les dispositifs de présentation souffrent souvent d'un problème fondamental : les éléments qui représentent les données (qu'il s'agisse ou non des valeurs numériques) que l'on veut présenter ne ressortent pas suffisamment en comparaison des autres éléments (cadres, lignes de référence, étiquettes), qui doivent certes être présents mais qui ne doivent pas masquer les données ou détourner l'attention de celles-ci.

Il faut donc autant que possible éliminer les éléments non directement liés aux données qui peuvent être source de distraction ou qui rendent plus difficile la lecture des données. Ainsi, il convient de réduire la redondance et l'encombrement. Il faut également éviter d'obliger le regard du lecteur à effectuer un va-et-vient continuel entre divers éléments du dispositif, ou entre celui-ci et la légende.

Pour un tableau, on prendra un soin particulier à éliminer les colonnes qui ne sont pas essentielles pour illustrer le phénomène que les données illustrent. On veillera aussi à arrondir les valeurs numériques en gardant le minimum de chiffres significatifs permettant de distinguer les valeurs les unes des autres. Finalement, on séparera les lignes en groupes de cinq environ, séparés par des espaces. Finalement, on pourra utiliser des éléments graphiques (gras, encadrés ou autres) pour attirer l'attention sur certaines valeurs particulièrement significatives.

Les tableaux 1 et 2 présentent deux versions du même tableau; les consignes précédentes ont été appliquées au second.

Tableau 1
Répartition en pourcentage de la population de 15 ans et plus
selon le niveau de scolarité et la région administrative, Québec, 1999.

Tableau 2
Répartition en pourcentage de la population de 15 ans et plus
selon le niveau de scolarité et la région administrative, Québec, 1996
(mêmes données qu'au tableau 1, présentation améliorée)

On remarquera que dans le tableau 2, on a classé les régions par ordre décroissant de pourcentage de détenteurs d'un grade universitaire, colonne qui a par la même occasion été mise en premier. Ce choix est relié au contexte d'utilisation de ce tableau, inclus dans un dossier proposant un nouveau programme de baccalauréat à distance, accessible dans tout le Québec. Notons qu'on a ajouté la moyenne provinciale, en la plaçant dans l'ordre avec les données des régions et que, pour chaque classe de scolarité, on a mis en évidence, en les encadrant par les signes mathématiques « ++ » et « -- », les valeurs minimale et maximale, quand celles-ci se démarquent suffisamment, en plus ou en moins, de l'ensemble des valeurs de la même colonne.

Certains pourraient hésiter à arrondir ainsi les valeurs, alors qu'elles sont en principe beaucoup plus précises (du moins on le suppose) que ce qu'affiche le tableau. Par exemple, on trouve que 5 régions présentent le même pourcentage (8 %) de détenteurs de grade universitaire. Mais est-ce vraiment imporant, pour les fins de la comparaison globale entre les régions du Québec, de savoir que Chaudiêres-Appalaches en compte 8.10% et Saguenay-Lac-Saint-Jean 8,16?

Pour ce qui est des graphiques, il faut veiller à ce que les éléments (étiquettes, quadrillage, légende, etc.) autres que ceux qui représentent des données prennent une importance démesurée, tant par leur la taille que par leur nombre ou leur simple présence visuelle. La figure 2 présente un graphique où les données (les points) ne sont pas vraiment en évidence et où le lecteur doit consulter la légende pour se souvenir de la signification des deux types de points et le texte pour savoir en quoi consistent les deux essais (voir la figure 4 pour version améliorée de ce même graphique).

Figure 2. Exemple d'un graphique accordant trop d'emphase aux éléments autres que ceux qui représentent les données.

Principe n° 3

La simplicité est de mise.

Les logiciels les plus utilisés pour générer des graphiques sont les chiffriers comme Excel, qui proposent des formats prédéfinis. Cependant, ceux-ci correspondent davantage aux pratiques en cours dans le domaine du marketing que dans le monde des sciences. Cela donne souvent des dispositifs artificiellement complexes qui ne font que déformer la nature des résultats, compliquer leur interprétation ou simplement ajouter de l'information inutile.

Par exemple, Excel propose des diagrammes où les valeurs sont représentées par des objets tridimensionnels vus en perspective (figure 3).

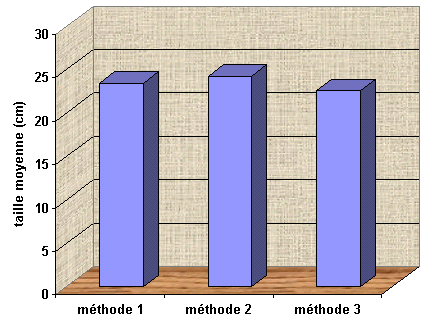
Figure 3. Exemple d'un diagramme dont les caractéristiques ajoutent de l'information nuisant à la lecture des données.

Or, une valeur numérique peut être représentée par un simple point sur un graphique. La représenter comme une boîte ou une pointe de tarte vus en perspective n'ajoute aucune information et, surtout, rend plus difficile tant sa lecture que sa comparaison avec d'autres valeurs.

Les logiciels spécialisés de graphiques scientifiques sont mieux adaptés à la production de graphiques conformes aux normes en usage en science. Malgré tout, il demeure possible de générer des graphiques acceptables avec un chiffrier tout usage comme Excel, à condition de n'utiliser que les modèles de base (appelés histogrammes et nuages de points dans le logiciel) et de modifier considérablement les options des modèles proposés. C'est d'ailleurs le moyen que j'ai utilisé pour l'immense majorité des dispositifs graphiques figurant dans ce cours.

Par ailleurs, quand le nombre des valeurs est peu important, une simple juxtaposition des valeurs dans un tableau est préférable à un dispositif qui fait en sorte que la plus grande partie de la tâche du lecteur consistera... à interpréter le dispositif lui-même plutôt que lire les données. En voici une illustration, qui reprend les mêmes valeurs que le diagramme de la figure 3, dont on peut décidément questionner l'utilité.

Taille moyenne des plantes

méthode 1 : 23,4 cm
méthode 2 : 24,2 cm
méthode 3 : 22,5 cm

moyenne générale : 23,4 cm

Principe n° 4

Il faut rechercher l'équilibre entre la présentation des valeurs numériques elles-mêmes et celle du phénomène ou de l'interprétation que ces valeurs éclairent ou suggèrent.

La présentation de résultats la plus appropriée n'est pas nécessairement celle qui permet de lire de la façon la plus précise les valeurs qui les composent. C'est plutôt, bien souvent, celle qui suggère ou appuie l'interprétation que l'on en propose, qui met en évidence le phénomène en cause et qui montre dans quelle mesure les valeurs affichées participent à ce phénomène.

Ainsi, le graphique de la figure 4 attire moins l'attention sur les points eux-mêmes que sur des courbes illustrant la tendance générale des données et faisant apparaître clairement que certains points ne sont pas cohérents avec l'ensemble. Souvent, ces courbes de tendance sont fondées sur un modèle mathématique décrivant ou expliquant le phénomène; on parle alors de courbes théoriques. Le graphique permet alors d'obtenir une représentation visuelle de l'adéquation du modèle aux données expérimentales.

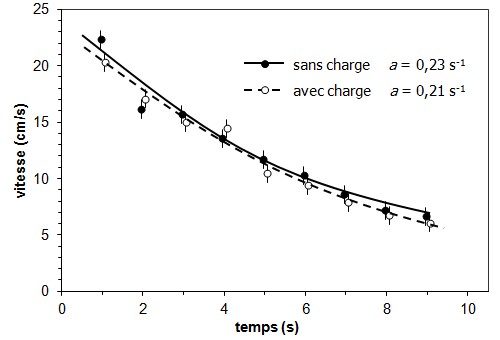
Figure 4. Exemple de graphique accordant de l'importance à des éléments facilitant l'interprétation des données (ici, des courbes théoriques). Les données sont les mêmes qu'à la figure 2.