|
|
|
|
|
1.
|
Introduction
|
|
La plupart des recherches en sciences, et
même dans les autres domaines, font intervenir la
détermination de caractéristiques mesurables
(appelées aussi grandeurs) des objets soumis à
l'étude. Mais à quel point peut-on mesurer la
véritable valeur d'une caractéristique? La
notion de « vraie » valeur a-t-elle
même un sens?
La réponse à ces questions fait
intervenir deux dimensions distinctes :
|
|
-
|
les caractéristiques d'un objet
ne sont jamais parfaitement définies ni
complètement stables; toute impression contraire peut
être démentie par le recours à des
méthodes ou des instruments de mesure suffisamment
sophistiqués;
|
|
-
|
les processus de mesure
possèdent des capacités limitées de
cerner les caractéristiques qu'il doivent mesurer;
ces processus comprennent l'appareil de mesure et ses
conditions d'utilisation.
|
|
Ces deux dimensions conduisent à des
interprétations différentes des valeurs
fournies par une mesure. Il n'existe pas de façon
générale de déterminer la part de
chacune dans une situation donnée; cependant, dans
bien des cas, une des deux domine suffisamment pour qu'on
puisse ne considérer que celle-ci.
Note. On retrouve dans les documents
disponibles en ligne un grand flou terminologique touchant
les concepts de précision, d'exactitude, de justesse
et de fidélité. Pour les trois derniers, nous
avons retenu les définitions du Vocabulaire
international de métrologie – Concepts
fondamentaux et généraux et termes
associés (VIM); le concept de précision
n'y est pas défini. Soulignons aussi que selon ce
même document de référence, l'expression
anglaise « measurement
precision » se traduit par
« fidélité (de mesure) »
et non par « précision », ce qui
est aussi susceptible de créer une certaine
confusion.
|
|
2.
|
Bonne définition et stabilité
des caractéristiques d'un objet
|
|
Certaines
caractéristiques possèdent une valeur
très bien définie, par exemple la masse d'une
plaque de métal. Une balance de bonne qualité
nous fournira cette valeur.
On pourrait croire qu'il en va de même
de son épaisseur; un appareil de mesure de
qualité nous apprendra qu'elle vaut, disons, 20,00
mm. Mais la mesure de l'épaisseur de la plaque en
quelques endroits (par exemple aux quatre coins et au
centre) pourrait révéler que cette
épaisseur varie légèrement sur la
surface de la plaque, par exemple entre 19,87 et
20,12 mm.
|
|
D'autres exemples :
|
|
-
|
la même plaque, placée à
l'extérieur en hiver, qui verra ses dimensions
diminuer légèrement à cause du
phénomène de dilatation/contraction du
métal avec la température;
|
|
-
|
le poids d'une personne, qui fluctue au cours
d'une journée (d'où la suggestion de se peser
à chaque jour au même moment, sur une
période de quelques semaines, si l'on veut savoir si
l'on prend réellement du poids).
|
|
Seules les mesures de type
dénombrement (compter des choses), et là
encore si les conditions sont idéales (objets
facilement distinguables, pas trop mobiles) échappent
à cette limitation. Si vous comptez sept objets,
cette « mesure » vaut exactement 7.
|
|
Sauf dans ce derniers cas, une mesure se
traduit donc par une série (ou éventail) de
valeurs. Ces valeurs forment une distribution,
c'est-à-dire qu'elles se répartissent selon
certaines proportions tout le long de l'éventail, en
étant généralement concentrées
autour d'une valeur centrale. Par convention, on peut
considérer cette valeur centrale comme la
« vraie » valeur de la
caractéristique. La figure 1 illustre trois
exemples de mesures qui fournissent des éventails
plus ou moins grands de valeurs pour une même
caractéristique, par exemple l'épaisseur de
plaques de métal plus ou moins
régulières.
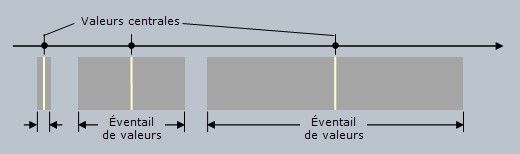
Figure 1. Représentation de
la distribution des valeurs d'une caractéristique
plus ou moins bien définie ou stable. La valeur
centrale (ligne jaune) est considérée comme la
« vraie » valeur.
La description détaillée de
cette distribution de valeurs ne peut se faire qu'à
l'aide d'un dispositif graphique, tel un histogramme ou un
diagramme à boîtes (voir texte
C6). Néanmoins, on peut en fournir une
description simplifiée à l'aide d'un nombre
restreint de valeurs; par exemple, on peut indiquer, au
moyen de ses valeurs minimale et maximale, l'intervalle qui
comprend toutes les valeurs possibles, ou encore une grande
partie d'entre elles.
Ainsi, on pourrait écrire que la
longueur d'un objet varie (ou se situe) entre 2,6 cm et
2,8 cm, par exemple dans le temps, ou selon
l'emplacement précis où l'on prend la mesure,
ou encore selon des facteurs externes comme la
température ou la pression atmosphérique.
|
|
3.
|
Précision du processus de mesure
(résolution et fidélité)
|
|
Tout processus de mesure est
caractérisé par sa précision,
définie ici comme la plus petite variation de la
valeur d'une caractéristique, supposée stable
et bien définie, qui peut être
détectée de manière reproductible par
ce processus. Cette précision
dépend :
|
|
-
|
de l'appareil de mesure : sa
qualité, sa sophistication, son état;
|
|
-
|
des conditions de son utilisation, ce
qui comprend la compétence, l'habileté et le
degré d'attention de la personne qui l'emploie.
|
|
La part de la précision liée
à l'appareil de mesure combine deux
facteurs :
|
|
-
|
la résolution de l'appareil,
qui est la plus petite différence de valeur
observable sur son affichage;
|
|
-
|
sa fidélité, soit sa
capacité de fournir la même valeur, ou des
valeurs très voisines, lors de mesures individuelles
successives de la même caractéristique,
effectuées sous les mêmes conditions.
|
|
Notons que la précision, telle que
définie ici, n'est pas liée à la
capacité du processus de mesure de fournir une valeur
identique ou proche de la vraie valeur; cette
capacité est la justesse, que nous examinons
plus loin.
La figure 2 représente une
série de mesures individuelles (rectangles n°1,
n°2, n°3, etc.) d'une même
caractéristique. La largeur des rectangles
représente la résolution de l'appareil; les
points (sur l'axe et au centre des rectangles) sont les
valeurs affichées. La figure illustre aussi la
moyenne des valeurs affichées. La variation
des valeurs successives traduit le degré de
fidélité de l'appareil.
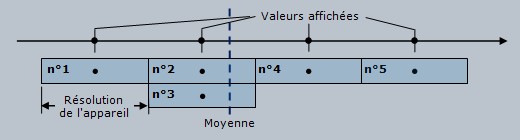
Figure 2. Représentation de
mesures individuelles successives et résolution de
l'appareil de mesure.
La figure 3 illustre trois mesures (en fait,
des séries de mesures individuelles) d'une même
caractéristique effectuées avec trois
appareils de résolution identique mais de
fidélité différente. En a), l'appareil
a une faible fidélité : 12 mesures
individuelles fournissent une large gamme de valeurs
(positions horizontales des points). En c), l'appareil a une
fidélité intermédiaire : les
mesures individuelles s'écartent beaucoup moins les
unes des autres qu'en b), si l'on ne tient pas compte de la
mesure n° 2. Une telle valeur, qui survient de
manière exceptionnelle, est appelée valeur
aberrante (outlier en anglais), et est en
général exclue de l'analyse. Finalement, en
c), toutes les mesures donnent le même résultat
: l'appareil est d'une excellente
fidélité.
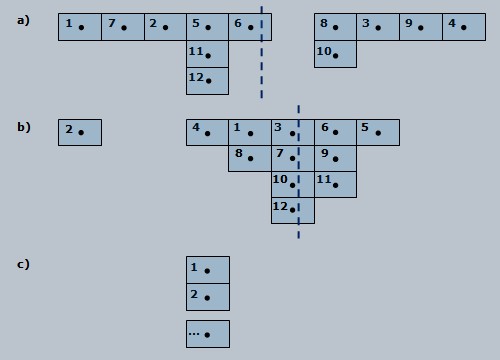
Figure 3. Comparaison de la
fidélité de trois processus de mesure, avec
des appareils de même résolution. En a), la
fidélité est plus faible qu'en b), où
l'on ne considère pas la valeur n° 2,
aberrante. En c), la fidélité est excellente
(ou parfaite). Les lignes pointillées sont les
moyennes des valeurs affichées.
Pour un appareil simple comme une
règle, c'est la résolution qui
détermine uniquement la précision; dans ce
cas, ou peut dire que la fidélité est
parfaite, car si celui qui effectue la mesure utilise la
même technique et demeure attentif, les mesures
individuelles successives sur un même objet (stable et
bien défini) donneront toujours le même
résultat.
Pour d'autres types de mesure, c'est
plutôt la fidélité qui détermine
la précision. Par exemple, mon pèse-personne
électronique affiche les 1/10 kg, ce qui correspond
à une résolution de 0,1 kg. Mais si je me
pèse plusieurs fois de suite, j'obtiens les trois
valeurs suivantes : 71,6; 71,7 et 71,8 kg. Dans ce cas,
même si l'appareil affiche une résolution de
0,1 kg, sa fidélité limitée
ramène sa précision à 0,3 kg. En
effet, puisque les valeurs 71,5 et 71,9 ne semblent jamais
apparaître, on peut conclure que mon poids se situe
probablement entre 71,55 et 71,85 kg.
La précision d'un appareil de mesure
est parfois indiquée dans le mode d'emploi de
celui-ci; cette précision est celle qui peut
être atteinte dans des conditions idéales par
un utilisateur expérimenté et attentif. Mais
la précision doit souvent, comme dans le cas de la
règle, être estimée de manière
plus ou moins subjective.
|
|
4.
|
Exactitude de la mesure
|
|
L'exactitude d'une mesure est la
correspondance entre la vraie valeur et la valeur
mesurée lors de l'application d'une procédure
de mesure donnée. La mesure peut être unique,
comme avec une règle. Elle peut aussi être
répétée; elle fournit alors un
éventail de valeurs, la valeur mesurée
étant prise comme la moyenne des mesures
individuelles.
Il faut distinguer les deux situations
suivantes :
|
|
-
|
la caractéristique mesurée est
bien définie, mais la précision du processus
de mesure laisse à désirer;
|
|
-
|
le contraire : soit une
caractéristique mal définie mais un processus
de mesure précis.
|
|
a)
|
Caractéristique bien définie /
processus de mesure peu précis
|
|
|
La figure 4 illustre les deux
premières mesures de la figure 3 (a et b), mais
en incluant la valeur réelle de la
caractéristique (ligne jaune), dont l'éventail
des valeurs (zone grise) est plus petit que la
résolution de l'appareil (rectangles bleus).
Si l'on considère dans chaque cas une
seule mesure, par exemple la mesure n°1, on peut dire
que cette mesure est beaucoup moins exacte en a) qu'en b).
Cependant, la notion d'exactitude ne présente pas ici
d'intérêt; autrement dit, si le processus a une
fidélité limitée, il ne faut surtout
pas se fier à une seule mesure.
Si l'on tient compte de l'ensemble des
mesures individuelles, on constate que la valeur obtenue
(moyenne des mesures individuelles) est plus exacte en a)
qu'en b), malgré une fidélité plus
faible en a).
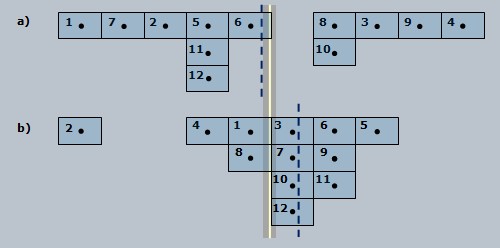
Figure 4. Mêmes mesures
qu'à la figure 3
(a et b), mais avec représentation de la vraie valeur
(ligne jaune). On constate que la mesure en a) est plus
exacte que la mesure en b), car la valeur moyenne (ligne
pointillée bleue) s'approche davantage de la vraie
valeur.
De son
côté, la justesse est l'exactitude
associée à un très grand nombre
(théoriquement infini) de mesures individuelles. Pour
chacune des deux mesures illustrées à la
figure 4, il se pourrait bien que l'ajout d'un grand
nombre de mesures individuelles supplémentaires en a)
et en b) modifie, dans un sens ou dans l'autre, la
correspondance entre la valeur mesurée et la vraie
valeur.
En ce sens, alors que l'exactitude est
associée à une application particulière
d'un processus de mesure, par exemple comprenant un nombre
limité de mesures, la justesse (tout comme la
précision) est une propriété du
processus de mesure lui-même.
|
|
b)
|
Caractéristique mal définie /
processus de mesure précis
|
|
|
Dans ce cas, on obtient encore un
éventail de valeurs, mais qui ne provient pas
principalement cette fois du processus de mesure. La
figure 5 présente deux mesures d'une même
caractéristique mal définie, effectuées
à l'aide d'un appareil de bonne résolution et
d'excellente fidélité (des mesures
individuelles répétées d'une
caractéristique bien définie donneraient
toujours la même valeur, comme dans la figure 3c).
On constate qu'un petit nombre de mesures
individuelles risque de ne révéler qu'une
partie de l'éventail des valeurs de la
caractéristique, et de fournir une valeur moyenne
erronée (figure 5a), donc une mesure peu exacte. Pour
mieux connaître l'éventail des valeurs, tout en
améliorant l'exactitude, il faut augmenter le nombre
de mesures individuelles (figure 5b). Cependant,
au-delà d'un certain nombre, qui dépend de
manière complexe des valeurs respectives de la
résolution, de la fidélité et de la
distribution des valeurs, l'ajout de mesures individuelles
supplémentaires n'apporte plus d'amélioration
significative.
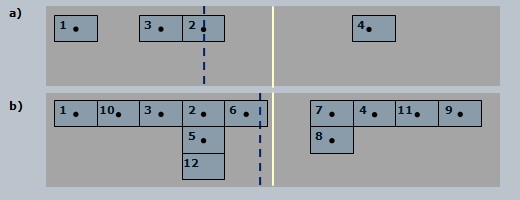
Figure 5. Effet du nombre de mesures
individuelles distinctes sur l'exactitude de la mesure d'une
caractéristique mal définie ou instable (zone
grise). Avec quatre mesures individuelles (a),
l'éventail des valeurs est sous-estimé, et la
moyenne est moins proche de la vraie valeur (ou valeur
centrale : ligne jaune) qu'avec 12 mesures
(b).
Pour reprendre l'exemple de la plaque de
métal, supposons que l'on a mesuré son
épaisseur en dix endroits avec un appareil
très précis, obtenant des valeurs variant
entre 1,977 et 2,038 cm, avec une moyenne de 2,012 cm. On
continue les mesures, jusqu'à 100, et on obtient des
valeurs comprises entre 1,976 et 2,040, pour une moyenne de
2,014 cm. Mais si on continue encore, jusqu'à
1 000 mesures, il est fort possible que ces
valeurs demeurent à peu près
inchangées.
|
|
5.
|
L'erreur systématique
|
|
Quelle que soit sa précision, un
appareil peut être défectueux, ou mal
étalonné, ou encore être mal
utilisé. Par exemple, la longueur de l'échelle
d'une règle peut différer de celle d'une
règle étalon; cela se produit, par exemple,
avec les règles de plastique, qui peuvent se
contracter avec le temps. Ou encore, la personne qui
l'emploie peut aussi le faire incorrectement, par exemple en
alignant le bord de la règle, et non le zéro
de l'échelle, avec le bord de la plaque.
La même chose peut se produire avec un
appareil à affichage numérique, qui peut ne
pas indiquer zéro pour une mesure de valeur nulle, ou
encore afficher des valeurs multipliées, par rapport
aux « vraies » valeurs, par une
constante ou une fonction dont la valeur demeure proche de
l'unité.
Il peut aussi arriver qu'un changement
apporté à un montage en cours
d'expérimentation vienne modifier un paramètre
influençant les mesures.
Dans tous ces cas, il se produit une
déviation par rapport à la valeur qui serait
normalement mesurée; cette déviation,
appelée erreur systématique, affecte la
justesse de la mesure, c'est-à-dire que la même
déviation se produira à toutes les
répétitions d'une même mesure, et se
répercutera directement dans la valeur de la
moyenne.
Les erreurs systématiques sont souvent
difficiles à détecter a priori, mais le
caractère systématique de la déviation
fait en sorte qu'elles peuvent, dans les cas les plus
simples, être déduites a posteriori à
partir d'un examen de l'ensemble des mesures. Il est alors
possible de rectifier les valeurs mesurées,
complètement ou partiellement, en leur apportant une
correction compensant pour l'erreur systématique.
Dans d'autres situations, un réexamen du montage
permet parfois de trouver la source de l'erreur et
d'évaluer directement la correction à
effectuer.
Par exemple, pour une règle, si
l'erreur systématique provient du fait que la
personne qui a fait la mesure a employé le bord de la
règle au lieu du début des graduations, il est
facile de la corriger. Il suffit de mesurer à quelle
distance du bord de la règle commencent les
graduations ou encore, si la règle n'est plus
disponible, de comparer une des mesures effectuée
avec cette règle la même mesure
effectuée correctement; il n'y plus alors qu'à
ajouter la même quantité de toutes les mesures
ainsi effectuées.
Reprenant l'exemple évoqué
plus haut, soit une plaque de métal
épaisse (en moyenne) de 5,924 cm. Un
expérimentateur sérieux utilisant correctement
sa règle obtiendrait 5,9 cm; son collègue
qui n'alignerait pas la règle sur le zéro des
graduations pourrait obtenir plutôt 5,7 cm,
mesure de même précision que la
précédente (égale à la
résolution de la règle) mais moins juste. Si
ce collègue a effectué de nombreuses mesures
à différents emplacements sur la plaque, et
qu'il n'a pas changé pas sa façon d'aligner la
règle au cours de ses mesures, il ne serait pas
nécessaire de les reprendre; il suffirait de corriger
toutes les valeurs qu'il a obtenues en leur ajoutant
0,2 cm.
Autre exemple, si vous vous pesez à
tous les matins en pantoufles et robe de chambre, la mesure
de votre poids sera entachée d'une erreur
systématique, que vous pourriez corriger en
soustrayant le poids de ces vêtements.
Un exemple célèbre d'erreur
systématique qui a pu être ainsi
corrigée concerne le télescope spatial Hubble.
Un des miroirs du télescope avait été
mal placé à cause d'une erreur
systématique de mesure dont la valeur a pu être
établie a posteriori, à partir de l'examen de
certaines parties du montage ayant servi à la
fabrication de l'instrument. Cette erreur,
détectée dès que le télescope a
fourni ses premières images, a pu être
corrigée par l'ajout d'une lentille de correction
lors d'une mission de maintenance qui a eu lieu deux ans
après son lancement.
|
|
6.
|
L'incertitude expérimentale
|
|
L'incertitude expérimentale est la
grandeur de la variation aléatoire,
imprévisible ou indéterminée, de la
valeur mesurée d'une caractéristique d'un
objet. Comme on l'a vu plus haut, dans bien des cas cette
variation est associée de manière dominante
à l'une ou l'autre des dimensions
suivantes :
|
|
-
|
la précision (résolution et/ou
fidélité) limitée du processus de
mesure (on parle alors d'incertitude de mesure);
|
|
-
|
l'instabilité,
l'irrégularité ou la mauvaise
définition de l'objet (incertitude
définitionnelle).
|
|
Mais comment, dans une situation
donnée, déterminer si une des dimensions
domine et, le cas échéant, laquelle?
Lorsque l'application d'un processus de
mesure ne fournit qu'une seule valeur, on peut conclure que
la dimension dominante est la précision du processus,
limitée par la résolution de l'appareil.
Mais si l'on obtient des valeurs
différentes lors de mesures successives, il n'existe
pas de méthode permettant de déterminer si
l'une des deux dimenstions domine, et encore moins
laquelle.
Heureusement, dans bien des cas, notre
connaissance préalable de l'objet ou du
phénomène mesuré et(ou) du processus de
mesure, de même que notre expérience
générale de ce type de mesure, permettent de
tirer des conclusions plausibles à cet
égard.
Par exemple, si l'on pèse un bloc de
métal à plusieurs reprises, il est clair que
toute variation significative dans la valeur obtenue
provient du processus de mesure. C'est la situation
illustrée (dans une nouvelle fenêtre) à
la figure 4.
Précisions que cette conclusion est valide si la
résolution de l'appareil ne permet pas de
détecter la différence infime de poids due,
par exemple, aux empreintes digitales, si on a
manipulé le bloc entre les mesures, ou à la
poussière qui a pu s'y déposer.
Par contre, si on mesure un courant avec un
multimètre que l'on a déjà
employé et dont l'affichage est habituellement
stable, des valeurs qui fluctuent de manière
substantielle amèneront à conclure que c'est
le courant lui-même qui varie. C'est la situation
illustrée à la figure 5.
On exprime une valeur mesurée
affectée d'une incertitude sous la forme
suivante :
valeur ± incertitude
Dans les deux exemples décrits plus
haut (longueur entre 2,6 et 2,8 cm et poids entre 71,55
et 71,85 kg), on écrirait :
longueur =
2,7 ± 0,1 cm
poids =
71,7 ± 0,15 kg
Il n'est pas toujours nécessaire
d'indiquer explicitement l'incertitude. Cependant, on doit
toujours le faire implicitement, au moyen du nombre de
chiffres significatifs que l'on affiche. Ainsi, telle que
mesurée avec une règle ordinaire,
l'épaisseur de la plaque de métal
décrite
plus haut, dont
l'épaisseur varie entre 1,977 et 2,038 cm, pourrait
s'écrire 2,0 cm, 20 mm ou 0,020 m
(notez la façon d'écrire ces trois variantes,
toujours avec deux chiffres significatifs). De même,
écrire que la longueur vaut 2,7 cm
suggère qu'on ne connaît pas la valeur de la
seconde décimale; sinon, on écrirait
2,70 cm, pour signifier qu'on sait que la longueur
n'est pas 2,72 ou 2,67 cm.
Pour des explications et des consignes sur
les chiffres significatifs et l'arrondissement des nombres,
consultez le document
suivant (dans une nouvelle fenêtre).
Quelle que soit sa source, l'incertitude ne
peut jamais être éliminée de
l'expérimentation et, contrairement à l'erreur
systématique, elle ne peut être
corrigée. Tout ce qu'on peut espérer est la
réduire, mais surtout à bien l'évaluer,
afin qu'elle se reflète correctement dans les
résultats et qu'elle soit prise en compte dans leur
interprétation.
|

|
|